Thermera の二色温度計測原理


Thermera(サーメラ)は、2色式アルゴリズムを採用した温度計測システムです。
放射率による補正をキャンセルし精度の高い温度計測ができます。
ガラス越し・非接触で温度計測でき、温度計測の課題を解決に繋がります。
1:2 色法の概念的理解
物体からの電磁放射(光等)は物体の温度が高くなるに従って
- 放射量が増大する(可視光域では輝度が高くなる)
- 最大の放射が成される波長が短くなる(可視光域では赤色から青白い色になる)
ことが知られています。黒体についてこれを図示すると 1-1 図の様になります。
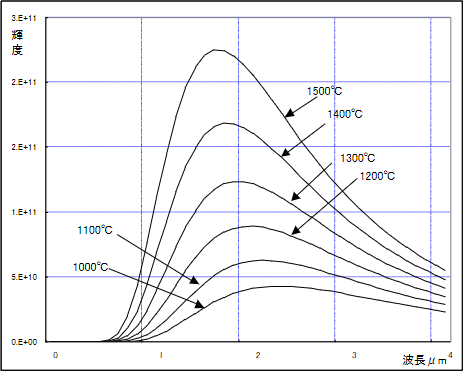
1-1 図 黒体放射の温度による変化
1-1 図の放射の曲線は、温度に対して 1:1 で対応しています。つまり温度によって曲線が全て異なります。これにより、ある温度の黒体の放射に関してこの曲線、即ち分光分布特性がどれであるかを計測すれば、温度を知ることができます。
レシオ温度はこの曲線を特定する方法として、二つの波長における放射を測定し、その比を算出します。この値は各黒体温度に対して、固有で一つの数値しかありませんので、これより温度を知ることができます。二つの波長の輝度を比較するところから、二色温度と呼ばれることもあります。
一般の物体は黒体ではありませんので、その物体が黒体と同じ温度である時の放射量は、黒体のそれより小さくなります。そしてその両者の放射量の比が放射率εであり、εは常に 1 以下となります。放射量から温度計測を行う場合、放射率を知ることが非常に重要ですが、放射率はその物体の物質表面の形状等によって異なる他、温度によって、波長によっても異なります。従って、被検体からの放射の強さを測定する輝度温度計や全放射温度計(赤外温度計等)で正確な温度測定を行うことは極めて困難です。
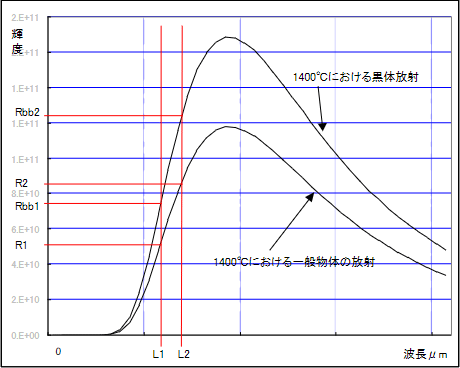
1-2 図 比温度の計測方法
これに対してレシオ温度計では、測定する物質の二波長の放射率が同じとなるような波長帯域を選べば、放射率が自動的にキャンセルされますので、その影響を受けません。その理由は 1-2 図で理解ができます。
般物体および黒体の分光放射のうち、波長 L1 と L2 の輝度に着目します。
一般物体の放射分布のうち L1 と L2 を接近して選ぶと、両者の放射率はほぼ同じになると考えられます。その関係が成立する限り、以下の関係が成立します。
つまり一般物体において、両波長の放射率が等しいという前提が成り立つ限り、その輝度の比は、黒体における両波長の輝度の比に等しいという関係が成立します。
また物体と測定システムの間にガラスや煙、水等が存在してその透過率が等しくτとした場合は
となり透過率の影響を受けません。
実際の測定においては、測定対象の輝度の比を求め、予め測定しておいた黒体の輝度の比と比較し、値が等しくなるところの黒体の温度が一般物体の温度になります。
これにより、2 色法は物体の放射率を知る必要がなく、また測定体と測定器の間にガラスや煙等両波長で透過率の等しい物質が介在しても、正確な温度測定が可能となります。
2:2 色法の数式的理解
2 色法は二つの波長における輝度温度を計測し、両者の比率をとることで、温度を求めます。
輝度温度は Planck の公式(3)により求められます。
物体からの電磁放射(光等)は物体の温度が高くなるに従って
ここで
- c1:第一放射定数=2πc2h=3.741844X10-16[Wm2]
- λ :波長 μm
- c2 :第二放射定数=c h/k=1.438769X10-2[m K]
- T :絶対温度(Kelvin)
- C :真空中の光の速度
- h :プランクの定数
- k :ボルツマンの定数
物体の放射率をε、物体から測定システムまでの透過率をτとした場合は、
となります。計測する二波長は可視域の場合 0.4𝜇𝑚~0.7𝜇𝑚内の二波長が使用されます。
ウイーンの近似式を適用すると式(4)は(5)のようになります。
いま、波長λ0 を中心とした幅Δλの波長域での放射エネルギーを M0 とすると
一般物体からの放射エネルギーM0 は(6)式から
ここで
- β0:比例係数
- ε0:波長λ0 での放射率
- τ0:波長λ0 での即定点から物体までの空間透過率
波長λ1およびλ2における放射エネルギーを M1、M2 とすると 2 波長比 R は

となります。
ここで、Δλを比較的広い波長域の光λ1、λ2 としても、β1、β2 はほぼ等しくβ1/β2=1 となります。また物体から測定システムまでに介在するものの透過率が波長に対してあまり変動しない時はτ1/τ2=1 となります。この条件を(9)式に適応すると、
ここで定数 C3、C4 は
です。
(10)式から理解できるように、2 波長の放射量の比は、温度に比例します。
また物体の放射率に無関係であり、レンズやガラス、ガス等物体と測定システムとの間に介在するもの透過率にも影響されることがありません。
3:2 色式熱画像カメラシステム
Thermera システムは、固体影像素子を使用したカラービデオカメラもしくは 2 センサーカメラを使用し、その 2 波長の画像から 2 色法アルゴリズムにより温度を算出します。使用する光学系、カメラを用いて予め温度較正を行っておくことで、撮影画像から温度分布画像を得ることが可能となります。2 色法による温度計測は 2 波長における放射の比から温度を算出するものであるため、望ましい画像記録システムは観測する視野を面記録できるカメラであって、各画素について二つの波長における放射を記録できる構造を持つカメラであるということになります。以下にその概要を説明します。
2-1:単板(1)センサー方式の構造
単板カラー方式のカラーカメラは 3 板方式に比べてコストを安くできるため、ほとんどのコンシューマ用ビデオカメラで採用されています。また通常のカラー高速度カメラは、この単板方式となっています。第 2-1 図にその構造例を示します。

2-1 図 単板カラーカメラの構造
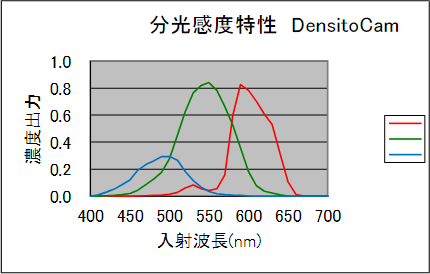
2-2 図 単板カラーカメラの分光感度特性
センサー各画素の前に赤、緑または青のフィルタが貼り付けられます。
従って、各画素は必要な赤、緑、青のうち一つしか持たないことになります。他の二つの信号は、周囲の画素から補完して作ることになります。例えば左から 3 列目上から上から 2 段目の画素は青の情報しかありませんが、緑は上下左右の緑画素の信号を加算平均して自己の緑色とし、斜めの赤4 画素の数値を加算平均して自己の赤とします。フィルタの配列と補完計算式には各社の工夫があり、カメラによって色の再現性は異なります。
2-2 図は DensitoCam カラーモデルの分光感度特性です。温度計測では RGB の出力のうち R および G の波長を用いて 2 色法で温度を算出します。B は波長感度が低いこと、R と G と比べかなりの高温でないと感光しないことから通常は使用しません。
2-2:2 センサー方式の構造
2 センサーカメラを用いる場合は、カメラユニットで入射光をビームスプリッタで 2 分光し、任意 の 2 波長のバンドパスフィルタを透過した画像を取得し、2 色法により温度を算出します。カラー カメラを用いる場合に対するメリットは、選択波長・波長巾を任意に設定することができるという ことです。例えば、熱放射以外の化学発光などがある場合、計測波長としてその発光波長以外を選 択することで、外的要因影響を避けた温度計測が可能となります。また、Si センサーの場合は最大 で 1μm、InGaAs センサーの場合は最大で 1.6μm までの波長感度を有しますので、カラーカメラ と比較して、より低温の計測が可能です。
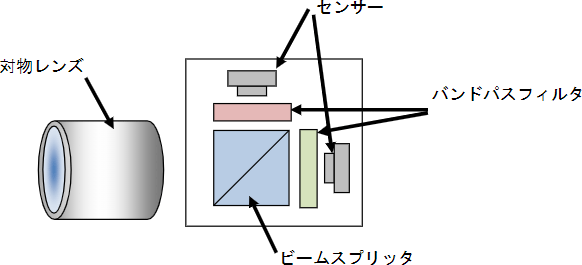
2-3 図 2 センサーカメラの構造
2-3:2 色式温度計測の基礎
波長λにおける放射輝度は、前述のように理論的には下記 Plank の公式は下記で示されます。
物体からの電磁放射(光等)は物体の温度が高くなるに従って
ここで
- C1:第 1 放射定数 =2πc2h=3.741844x10‐16 [wm2]
- λ:波長(m)
- C2:第 2 放射定数=c h/k=1.438769x102 [mk]
- T:絶対温度 [°K]
-
- C:真空中の光の速度
- h:プランクの定数
- k:ボルツマンの定数
この波長域における 500℃―3000℃の黒体放射の分布を算出すると 2-4 図のようになります。
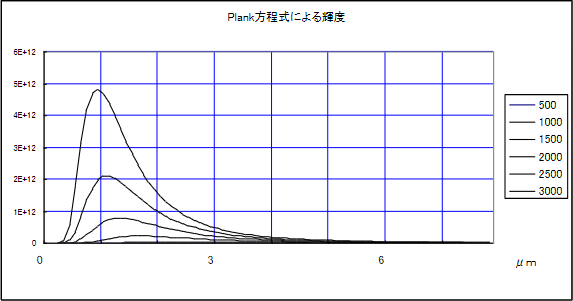
2-4 図 各温度における黒体放射の分布
この公式による可視光域の分布を見るために、人間の肉眼と通常の CCD/MOS 固体素子撮影カメラがカバーする可視光域 400-800nm(0.4~0.8μm)について算出プロットすると 2-5 図のようになります。
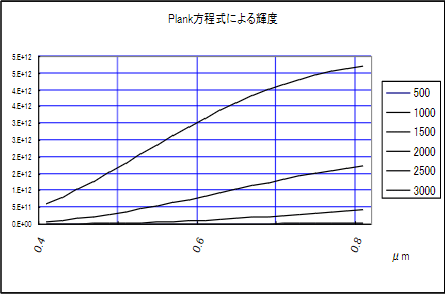
2-5 図 400‐800nm における各温度の黒体放射
この温度領域では放射のほとんどが可視光域外の赤外域に存在することが理解できます。従ってレシオ温度の計測に際してはより波長の長い(赤より)の光や近赤外光を利用することが効率的であることが分かります。
前述のように、レシオ温度を以下の式で求めることができます。
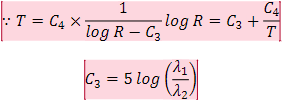
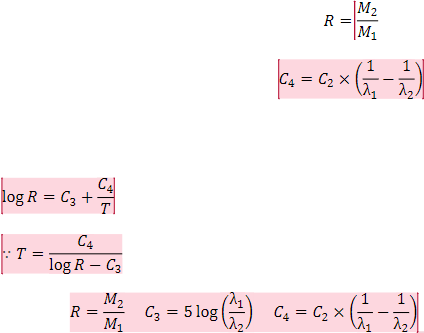
この温度領域では放射のほとんどが可視光域外の赤外域に存在することが理解できます。従ってレシオ温度の計測に際してはより波長の長い(赤より)の光や近赤外光を利用することが効率的であることが分かります。
前述のように、レシオ温度を以下の式で求めることができます。
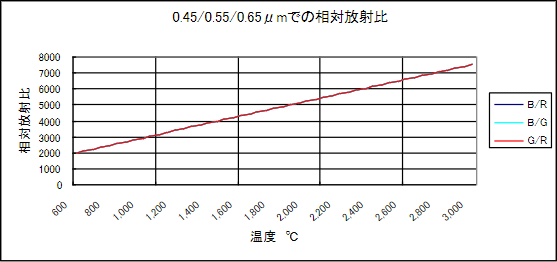
2-6 図
λ1=0.45μm λ2=0.55μm λ3=0.65μm とし
λ1/λ3、λ1/λ2、λ2/λ3 の相対放射比
当然のことながら、λ1/λ3、λ1/λ2、λ2/λ3 における、相対放射比は同じ値を示します。
2-6 図の計算は単波長について行われたものですが、現実には単波長のフィルタは存在せず、干渉フィルタは 1~40nm 程度の半値巾(減衰が 50%になる時の透過波長域巾)を持ちます。また実際のカラービデオカメラは、R、G、B について半値巾が各 40nm 程度のバンド巾を持ちます。
そこで同じ波長を中心として 40nm のバンド巾について計算し、プロットすると 2-7 図のようになります。
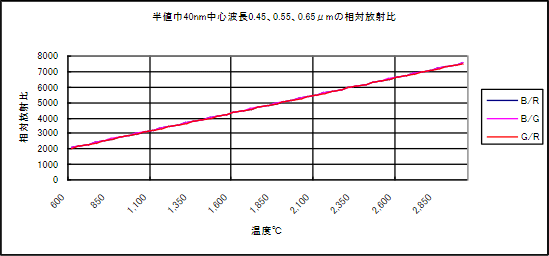
2-7 図 半値巾 40nm における相対放射比
この場合も単波長での計算と同様、各比率における温度は同じ値となります。
カメラの総合分光特性は、これにレンズの分光透過特性、フィルタの透過特性を総合したものになります。
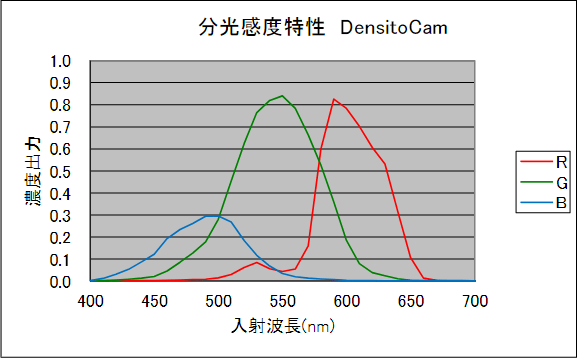
2-8 図 カラーカメラの総合分光特性例
2-8 図はカラーカメラの総合分光特性例です。R、G、B 各波長出力とも、単波長ではなく、一定の帯域幅を持っています。
この図より、B の中心波長は 490nm、G の中心波長は 540nm、R の中心は 590nm と考えることができます。
2-8 図のような分光特性をもった、カラーカメラについて、
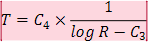
式により、2 色温度計測のシミュレーションを実行すると、2-9 図のようになります。 3 つのプロット結果が一致しないだけではなく、直線性がありません。
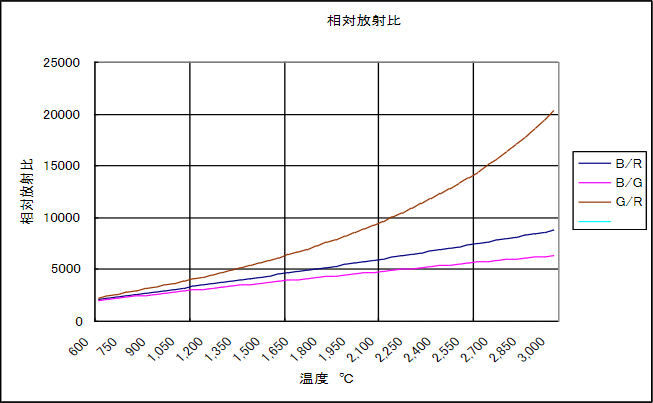
2-9 図 補正前の相対放射比
これを Thermera の補正ロジックで演算補正した後、温度を求めると、2-10 図のようになります。
B/R、B/G、G/R 時の算出温度値がほぼ一致すると同時に、計算値が温度に対してリニアであることが分かります。これより、一般のカラービデオカメラの出力を温度検出システムとして用いることに問題がないことが知れます。
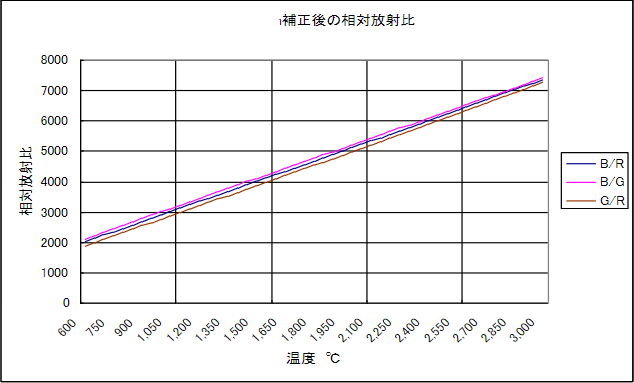
2-10 図 補正後の相対放射比

